EECS 349 Problem Set 3
Due 11:59PM Thursday May 14
Instructions
Answer clearly and concisely. Some questions ask you to "describe a data
set." These data sets can be completely abstract creations. Often it
will help to draw a picture. Your argument doesn't have to be rigorously
formal but it should be convincing. To give you an idea of what we're looking
for, consider the following sample question:
Sample Question: With continuous attributes, nearest-neighbor
sometimes outperforms decision trees. Describe a data set in which nearest
neighbor is likely to outperform decision trees.
Sample Answer: Consider a data set with two continuous attributes x1
and x2 which lie between 0 and 1, where the target function is "return 1
if x2 > x1, and 0 otherwise." Decision trees must attempt to
approximate the separating line x1 = x2 using axes-parallel lines (a
"stair-step" function), which will require many distinct splits.
Thus, decision trees will be inefficient at both training and test time, and
could be inaccurate if there isn't enough data to generate enough splits to
approximate the separating line x1=x2 well. On the other hand, the lines of
the Voronoi diagram in nearest neighbor can be parallel or nearly parallel to
the separating line x1 = x2, so with a reasonable number of training examples
we would expect NN to approximate the target function well.
This sample answer is not mathematically precise,
but it is plausible and demonstrates that the writer knows the key
concepts about each approach.
Questions
The questions are worth 10 points total.
Nearest Neighbor, Decision Trees, Neural Networks (3 points)
- (2 points)
Consider learning each of the four target functions given below. For three
of these functions, ONE of Nearest Neighbor, Decision Trees, or Neural Networks is likely
to perform best. For each of those three tasks, state which algorithm is best and briefly (1-2 sentences)
state why. For the remaining function, NONE of the learning algorithms is likely to perform
well. For this task, state why none of the algorithms will perform well. All concepts are
defined over binary inputs x1,...x100 and binary output y. The expression -x5 means
"not x5".
- y = 1 if (x1 AND x3 AND -x7 = 1) OR (x45 AND -x67 AND x90 = 1), and
y = 0 otherwise.
The training
data has 10,000 examples.
- For y=1, for each example each xi is independently randomly generated as: xi=1 with probability 0.55,
and xi=0 with probability 0.45. For y=0, the probabilities are flipped: P(xi=0 | y=0)=0.55 and P(xi=1 | y=0)=0.45.
The training
data has only 100 examples.
- y = 1 if the number of xi's equal to 1 is odd
y = 0 otherwise.
The training data has 10,000 examples.
- y = 1 if x3 + x5 + x20 + x21 - x22 + x88*x99 - x7*x8/(x3 + 0.1) > 0
y = 0 otherwise
The training
data has 10,000 examples.
-
(1 point) Give a data set for which 3-nearest neighbors is likely to perform
better than 1-nearest neighbor.
Perceptrons (1 point)
- (1 point) Draw a perceptron (with weights) that has two binary inputs A and B
and that computes A NAND B. That is, the perceptron outputs 0 if A=B=1, and 1
otherwise.
Optimization (3 points)
- (0.5 points) What's the key ingredient in GAs that distinguishes them from local beam search?
- (2.5 points) For each of the following approaches, give an example of an optimization problem which is more easily solved by that approach than by any of the other approaches. For each problem, explain why it's so well-suited for the approach you chose.
Note, for this question, you can choose in each case whether the function to be
optimized is known in mathematical form to the algorithm.
- Genetic Algorithms
- Gradient Descent
- Hill Climbing
Bayes Nets and Statistical Estimation (3 points)
Consider six binary variables related to scoring well on an exam:
G (got a good night's sleep),
S (studied a lot),
I (find the material interesting),
E (exam is easy),
A (got an A on exam),
R (recommend class to friends at end of quarter).
-
(1 point) Draw a Bayes Net representing this situation. There are multiple
different reasonable networks for this domain. You should try to exploit
conditional independencies and end up with relatively few edges.
-
(0.25 points) What is the minimum number of probabilities you would need in
order to specify all the conditional probability tables for your Bayes Net?
-
(0.25 points) How many independent parameters are needed to specify the full
joint distribution over the six variables?
-
(0.5 points) Using your network, is E (whether the exam is easy) independent of
G (whether you got a good night's sleep) when we are not given the value of any
other variables? In a sentence, justify why or why not.
-
(0.5 points) Using your network, assume we know A = true (you got an A on the
exam). Is E conditionally independent of G given A? In a sentence, say why or
why not.
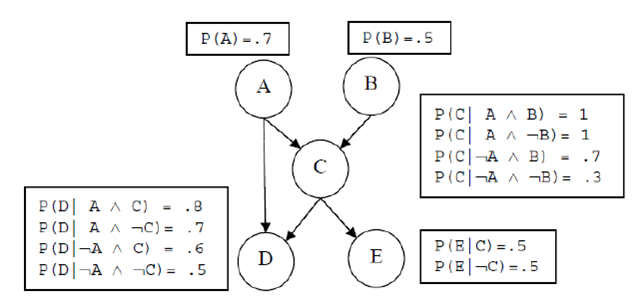
Consider the Bayes Net pictured below.
-
(0.25 point)
Suppose that the network was computed from maximum likelihood estimates
over a data set of ten examples.
Suppose we then see two more examples with A=1. What
will be the new maximum likelihood estimate for P(A)?
-
(0.25 point) What is P(C) for the below Bayes Net?
Show your work (hint: this should be about two lines of math). Note:
use the original value for P(A)=0.7 given below, not your updated answer from part a.