Please include a README.txt that has both partner's names and email addresses.

Your task is to implement the core of a Tsuro game administrator. The essence of the task is the design of data structures that represent the state of the game together with the design and testing of two key functions that operate on them: legal-play? and play-a-turn.

Make sure that your design is evident to readers of your code. Ensure you data structures are clearly described, your functions are small, well-named, organized neatly, and come with test cases.

Start by reading the rules.

The legal-play? function determines whether it is legal for a given player to place a given tile on a given board. There are two ways a tile placement can be illegal

1. the placement of the tile is an elimination move for the player (unless all of the possible moves are elimination moves), and
2. the tile is not (a possibly rotated version of) one of the tiles of the player.

Note that the use of the word "tile" here (and generally in this assignment) never refers to the dragon tile, only tiles that may actually be played on the board.

The signature of legal-play? should look like this, in a notation similar to Racket contracts (You do not need to use Racket for this task; I use it here only to bring a level of precision to the description of the assignment.)

legal-play? : splayer?
              board?
              tile?
              ->
              boolean?

The legal-play? function consumes three arguments: the player that attempts to place a tile, the board before the tile placement, and the tile that the player wishes to place on the board.

The correct implementation of legal-play? depends on the correct design of data structures for the player, the board and the tile. In particular the data structure for tiles must have enough information to distinguish a tile from any other tile, up to rotation. Similarly the data structure for players must carry the color and the list of tiles of a player, including the tile to be placed. Finally the data structure for boards must track the details of players and tiles on a board.

The play-a-turn computes the state of the game after the completion of a turn given the state of the game before the turn. It is called only if the given move is known to be legal. Here is its signature:

play-a-turn : (listof tile?)
              (non-empty-listof splayer?)
              (listof splayer?)
              board?
              tile?
              ->
              (listof tile?)
              (listof splayer?)
              (listof splayer?)
              board?
              (or/c #f (listof splayer?))

The function consumes five arguments and returns five results. The first argument is the list of tiles on the draw pile. The second argument is the list of players still in the game in the order of play and the third argument is the list of eliminated players in no particular order. The fourth argument is the board before the turn and the last argument is the tile to be placed on that board. Note that the tile to be placed on the board should have been removed from the list of tiles of the active player before calling the function. For example, before the first call of play-a-turn in a game, the first player in the second argument of the call (the players still in the game) should have 2 tiles, while all of the other players in that list should have 3 tiles.

The first result of play-a-turn is the draw pile after the turn. The second result is the list of players that are still in the game after the turn, in order of play for the next turn. For example, if no players gets eliminated in a turn, this result list is the one you get by taking the second input (the list of players that are still in the game) and moving the first player to the end of the list. The third result is the list of players that are eliminated after the turn in no particular order (including those that were already eliminated before the turn). The fourth result is the board after the turn and the last result is false when the game is not over or the list of players that, if the game is over.

The full set of tiles that are valid in any Tsuro game is encoded below in s-expressions showing the set of four paths that appear on the face of each tile. The end points of the paths are numbered according to this diagram:

        0   1
    +-----------+
    |           |
  7 |           |  2
    |           |
  6 |           |  3
    |           |
    +-----------+
        5   4

As an example, the first tile in the list looks like this: 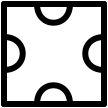and the last looks like this:

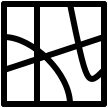
((0 1) (2 3) (4 5) (6 7))
((0 1) (2 4) (3 6) (5 7))
((0 6) (1 5) (2 4) (3 7))
((0 5) (1 4) (2 7) (3 6))
((0 2) (1 4) (3 7) (5 6))
((0 4) (1 7) (2 3) (5 6))
((0 1) (2 6) (3 7) (4 5))
((0 2) (1 6) (3 7) (4 5))
((0 4) (1 5) (2 6) (3 7))
((0 1) (2 7) (3 4) (5 6))
((0 2) (1 7) (3 4) (5 6))
((0 3) (1 5) (2 7) (4 6))
((0 4) (1 3) (2 7) (5 6))
((0 3) (1 7) (2 6) (4 5))
((0 1) (2 5) (3 6) (4 7))
((0 3) (1 6) (2 5) (4 7))
((0 1) (2 7) (3 5) (4 6))
((0 7) (1 6) (2 3) (4 5))
((0 7) (1 2) (3 4) (5 6))
((0 2) (1 4) (3 6) (5 7))
((0 7) (1 3) (2 5) (4 6))
((0 7) (1 5) (2 6) (3 4))
((0 4) (1 5) (2 7) (3 6))
((0 1) (2 4) (3 5) (6 7))
((0 2) (1 7) (3 5) (4 6))
((0 7) (1 5) (2 3) (4 6))
((0 4) (1 3) (2 6) (5 7))
((0 6) (1 3) (2 5) (4 7))
((0 1) (2 7) (3 6) (4 5))
((0 3) (1 2) (4 6) (5 7))
((0 3) (1 5) (2 6) (4 7))
((0 7) (1 6) (2 5) (3 4))
((0 2) (1 3) (4 6) (5 7))
((0 5) (1 6) (2 7) (3 4))
((0 5) (1 3) (2 6) (4 7))

Hand in this assignment via GitHub.