hw4

CS 115, Fall 2002
Homework Assignment 4
Due: 21 October 2002

Family Trees

Recall the data definition for family trees:

A family-tree is either:

'unknown
(make-ft name eye-color mom dad)
where name and eye-color are symbols,
and mom and dad are family-trees.

(define-struct ft (name eye-color mom dad))

Write a function called path-to-blue-eyes that finds a path to a blue-eyed ancestor, if one exists and returns #f if there aren't any. A path is represented as a list of symbols, either 'mom or 'dad.

Here are some examples (be sure to use these as tests when developing your function):

(define tutu (make-ft 'emily 'brown 'unknown 'unknown))
(define opa (make-ft 'bruce 'blue 'unknown 'unknown))
(define mom (make-ft 'alice 'green tutu opa))
(define dad (make-ft 'bill 'brown 'unknown 'unknown))
(define me (make-ft 'robby 'hazel mom dad))

(path-to-blue-eyes 'unknown) "should be" #f
(path-to-blue-eyes tutu) "should be" #f
(path-to-blue-eyes opa) "should be" '()
(path-to-blue-eyes mom) "should be" '(dad)
(path-to-blue-eyes dad) "should be" #f
(path-to-blue-eyes me) "should be" '(mom dad)

Solution

There is more than one solution to this problem, since there may be more than one path to a blue eyed ancestor and different functions may find different paths. Here's one solution:

;; path-to-blue-eyes : family-tree 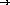 list-of-symbols or #f
;; finds the path to a blue eyed ancestor
(define (path-to-blue-eyes ft)
  (cond
    [(eq? ft 'unknown) #f]
    [else
     (if (eq? (ft-eye-color ft) 'blue)
         '()
         (let ([mom-path (path-to-blue-eyes (ft-mom ft))]
               [dad-path (path-to-blue-eyes (ft-dad ft))])
           (cond
             [(and mom-path dad-path) (cons 'mom mom-path)]
             [(and mom-path (not dad-path)) (cons 'mom mom-path)]
             [(and dad-path (not mom-path)) (cons 'dad dad-path)]
             [else #f])))]))

Sets

Write a function called union that computes the union of two sets. The union of two sets is a set that contains all of the elements in both sets.

Write your data definition for sets, along with any invariants of the data definition and be sure that your function satisfies those invariants.

Here is a function header for union

;; union : set-of-numbers set-of-numbers 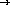 set-of-numbers
;; builds a set of the numbers contained in both \scheme|s1| and \scheme|s2|
(define (union s1 s2)
  ...)

Solution

Here are two possible solutions:

A set-of-numbers is either:

'()
(cons number set-of-numbers)

Invariant: the set of numbers does not contain any duplicates.

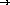;; union : set-of-numbers  set-of-numbers
(define (union s1 s2)
  (cond
    [(null? s1) s2]
    [else (let ([un (union (cdr s1) s2)])
            (if (number-in-set? (car s1) un)
                un
                (cons (car s1) un)))]))

;; number-in-set? number set-of-numbers 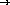 boolean
(define (number-in-set? num set)
  (cond
    [(null? set) #f]
    [else (or (= num (car set))
              (number-in-set? num (cdr set)))]))

A set-of-numbers is either:

'()
(cons number set-of-numbers)

Invariant: the set of numbers is in sorted order and does not contain any duplicates.

This function processes two complex forms of data simultaneously:

;; union : set-of-numbers 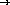 set-of-numbers
(define (union s1 s2)
  (cond
    [(and (null? s1) (null? s2)) '()]
    [(null? s1) s2]
    [(null? s2) s1]
    [else (let ([fst-s1 (car s1)]
                [fst-s2 (car s2)])
            (cond
              [(= fst-s1 fst-s2) 
               (cons fst-s1 (union (cdr s1) (cdr s2)))]
              [(< fst-s1 fst-s2)
               (cons fst-s1 (union (cdr s1) s2))]
              [(< fst-s2 fst-s1)
               (cons fst-s2 (union s1 (cdr s2)))]))]))

Last modified: Mon, Oct 28, 2002, 8:18 pm
HTML conversion by TeX2page 4p4k3