

Given E(u,v) and n(u,v), a silhouette point is defined as the point on the surface where E(u,v) . n(u,v)= 0 or the angle between E(u,v) and n(u,v) is 90 degrees, as shown in Figure 3.5.
Linear interpolation is done only in one parametric dimension, u or v, keeping the other constant. Given two surface points at parametric values t1 and t2, such that t1 = (t1, vo) and t2 = (t2, vo), can be defined by n(ti), the normal at ti, and E(ti), the eye vector, as seen in Equation 4.1.
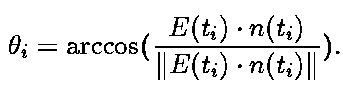
Given 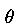 1 and
1 and 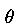 2 and the corresponding parametric
values, t1 and t2, linear interpolation will give an approximate
t* where the angle is 90 degrees or
2 and the corresponding parametric
values, t1 and t2, linear interpolation will give an approximate
t* where the angle is 90 degrees or 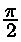 :
:
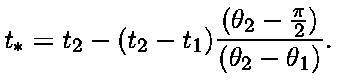
|
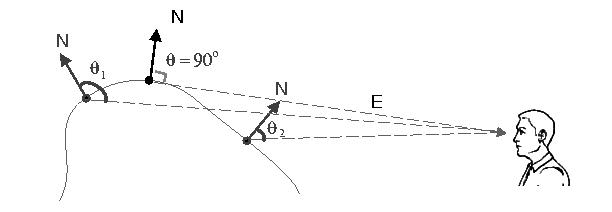
Figure 4.1:
Interpolating silhouettes: After two neighboring surface
points with different 's are found, the point where
E(u,v) . n(u,v) = 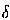 = 0 can be found by linearly interpolating in
u or v with the two angles as calculated in Equation 4.1.
Note: = 0 can be found by linearly interpolating in
u or v with the two angles as calculated in Equation 4.1.
Note: 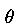 1 = (E1
. n1) is greater than 0 and 1 = (E1
. n1) is greater than 0 and 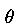 1 = (E2
. n2) is less than 0 . 1 = (E2
. n2) is less than 0 .
|