|
home
about
team
projects
papers
downloads
manual
messageboard |
Hunter-Runner: Implementing HIVEMind on FlexBot
Aaron
Khoo
The Search Algorithm
We conceive of the map as a
standard graph representation with nodes (waypoints)
and edges (connections between the waypoints). Waypoints are always
line-of-sight. The Runner and Hunters
know their starting locations, as well as the exit points. When the
Hunters start, their first priority is to travel to the exit points in
order to prevent the Runner from reaching its goal. There is at
least one Hunter per exit point. If there are more Hunters than exit
points, the leftover Hunters will arbitrarily pick an exit point. When
the Hunters arrive at the exit point, we can now view the graph with the
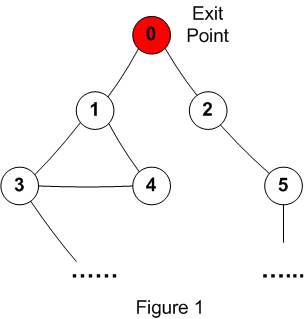
exit points as the root nodes. Figure 1 below shows a simple map with
one exit point at node 0.
 |
Now, the algorithm proceeds in the
following way:
- For the next level in the graph,
figure out how many corridors are there connected to nodes on
the current level. Right now, all the Hunters are currently
located at node 0, and there are two corridors leading out
from node 0. Therefore, node 0 requires at least two Hunters
to start.
- If the total number of required
Hunters is not enough (2 in this case), then we should just
halt here. We can't actively search the rest of the map
without exposing some path to the exit.
- If we have enough Hunters, then
move the Hunters into the appropriate starting positions.
Begin traversing the corridors after all the Hunters have
moved into the appropriate starting positions. So, one Hunter
traverses 0->1, and the remaining Hunters traverse
0->2.
|
 |
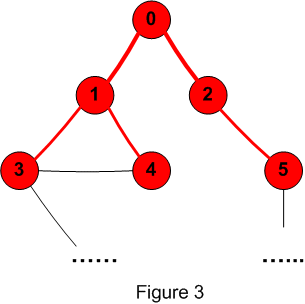
When all the Hunters have arrived at
either nodes 1 or 2, the algorithm simply repeats:
- Node 1 has two corridors extending
from it, and node 2 has one. So we need at least three Hunters
total to search the next level of the graph.
- If we don't have enough enough
Hunters, we should stop moving forward. We can't trap the
Runner, but at least we can prevent her from reaching the
exit.
- If we have enough Hunters, then
move two to node 1, and the rest to node 2. After they arrive,
traverse corridors 1->3, 1->4 and 2->5.
|
 |
Again, we keep repeating the algorithm
until all corridors have been searched, or the Runner is found and
trapped. The Runner can either be trapped in a dead end, or in a
corridor between two Hunters.
Obviously, this algorithm is
suboptimal. So we have a priori knowledge of the map, we can
actually pre-calculate an optimal search path through the graph
given the available number of Hunters. At present, time is wasted maneuvering
the Hunters into their initial positions before they traverse the
corridors.
However, the point of this experiment
is not to find an optimal search path through the graph. Rather,
it is to show the power of the communication architecture we have
utilized for this task. Furthermore, our communication
architecture supports the ability to dynamically add or subtract
team members during run-time. So the a priori calculation based on
the starting number of bots could be invalidated if the size of
the team changes during run-time. |
<<<<<
The Hunters | The HIVEMind
>>>>>
|


