 |
|
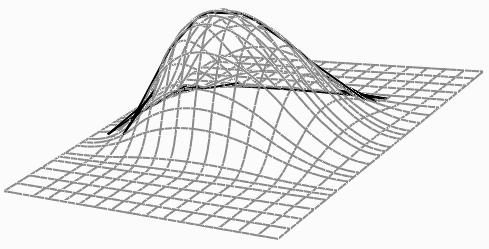
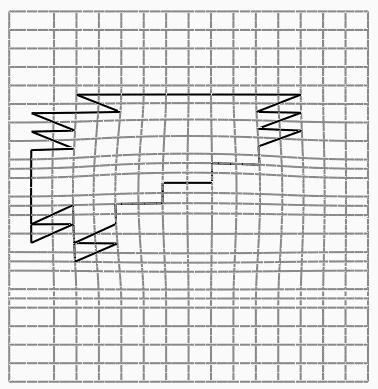
| View of surface with approximate silhouettes generated with the tessellated mesh method. | Looking down on surface with approximate silhouettes. |
| Figure 4.7: Tessellated Mesh Method. | |
A variation on the Mesh Method is the Tessellated Mesh Method. In order to simplify the number of possible sign combinations, I tessellated the control mesh. The control mesh of a surface is a set of bilinear patches. I split each of those bilinear patches into triangles by choosing the diagonals to be in the direction of minimum curvature across each bilinear patch. Then there is only one normal per triangle or two normals per bilinear patch. However, checking for silhouettes with these normals only tells one where a silhouette may be. After choosing the area that may have silhouettes, you then have to find the corresponding point on the surface and find the nearby silhouette point and curve if it exists. A winged-edge data structure can keep track of all of these data and is useful for turning silhouette points into silhouette curves. The only part left is to refine these jaggy lines as seen in Figure 4.7 into silhouette curves. I did not proceed past finding the approximate silhouette curves because this method was too slow.
 |

|
| View of surface with approximate silhouettes generated with the tessellated mesh method. | Looking down on surface with approximate silhouettes. |
| Figure 4.7: Tessellated Mesh Method. | |